Introduction

Resnet going deep

The conventional wisdom in machine learning now says that the future is with deep neural networks.

However, training deep neural networks has been tricky.

What is deep?

A breakthrough 2015 paper, [VGG], introduced networks with up to 19 convolution layers; as the name of this paper suggests, these networks were considered very deep.

Since then another breakthrough introduced a new type of architecture called residual networks, or resnets, which allowed training models of over 1000 convolutional layers; this breakthrough appeared in a series of two papers, [Resnet] and [StrictResnet].

This post reports on my attempts to train networks suggested by [StrictResnet]. I shall call them strict resnets.

What is in this post?

Besides reporting on my attempts to train such networks, I explain in depth how they work.

I start with studying the checkerboard phenomenon as it manifests in my tests.

I report on the dependence of my training results on initialization.

I have used Glorot and He initializations; these initialization techniques are currently standard.

I explain them in detail, including the purpose they were initially suggested, how they interact with batch normalization, and how they can affect strict resnets as I have observed.

Finally, I try to study the question whether deep is always better than wide. As one would expect, the answer is negative: at some point, the depth does not add and only consumes computational resources without improving the training results.

My data and challenge

I tried to participate in Kaggle TGS Salt Identification Challenge competition. It was an image segmentation challenge.

While other participants successfully used deep networks pretrained on large datasets, I did not want to follow this approach as I wanted to develop some other ideas which were incompatible with pretrained data.

For this reason, I tried to train strict resnets from scratch and found out that training such networks is not straightforward and requires attention to architecture and initialization.

My tools

My primary software tool was Keras; this is the reason I shall be referring to it below.

I ran my models on Nvidia Tesla K80 GPU on Google Compute Engine. Training of a typical deep model I used, took 6-10 hours on this equipment.

I tried to get a working model rather than to research how to train strict resnets. For this reason, the results I report here on comparison of different ways of training such networks are not always systematic.

It could be that the loss function I used, exacerbated the training phenomena I am reporting here. For the discussion, see below: My loss function may have strengthened…

Strict resnets

What they are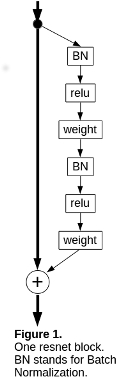

They are towers built of blocks similar to the one shown in Figure 1.

The information flows along the vertical line in Figure 1 and the contribution of each resnet block is added to it.

They never saturate

[StrictResnet] argues that such architecture ensures that networks built this way never saturate – there are no regions in the weight space in which the gradients of the outputs with respect to the weights vanish.

The argument goes as follows.

The mapping from the inputs of the model to the outputs is a composition of similar mappings for individual resnet blocks. The mapping from the inputs to the outputs of one resnet block is of the form I + F where I is the identity mapping and F is the contribution of the block: it is the composition of linear weight blocks, activations and batch normalizations that appear to the right of the vertical line in Figure 1.

Due to the presence of the identity term, the derivatives with respect to the weights may be close to zero at individual points in the weight space but not in any regions there.

It follows that the derivatives of their composition – the mapping from the inputs of the model to its outputs – do not vanish in any region of the weight space.

[StrictResnet] mentions that this argument works also in case we allow other terms in our composition which do not have saturation regions, provided they are not too many; the information would flow freely through such blocks even though it may change.

Specifically, this paper mentions projections to reduce the feature space, and embeddings to increase it.

I would also include here weight blocks – I used convolutions for my image segmentation challenge – and batch normalizations, but not activations as they may saturate. (If many weight blocks applied consecutively then for certain initializations such tower may saturate. We care not to apply too many – more than 4 – weight blocks consecutively.)

Changes in feature space

Each resnet block shown in Figure 1 operates in one feature space; the vertical line on Figure 1 is the identity mapping from the inputs to the outputs of this block, to which the contribution of the block is added. We shall assume that all layers of this block operate in the same feature space.

It is possible that the first weight block in Figure 1 maps the original feature space into another one, and the second weight block maps it back; [Resnet] discusses such architectures and calls them bottleneck. I have not tried such architectures.

Sometimes we need to change the feature space. For images, we may need to change the resolution of the image or the number of channels.

[StrictResnet] suggests adding or removing dimensions in such cases. In other words, if we need to reduce the feature space, we project it by removing some of the dimensions, and if we need to increase it then we embed it by adding new dimensions.

Such operations disrupt the identity mapping on the main information path; however, as we have mentioned, projections and embeddings do not have saturation regions, and, hence, they do not affect the above argument in favor of non-saturation.

For image models, reducing the feature space may mean either downsampling or decreasing the number of channels, and increasing the feature space may mean either upsampling (not present in [StrictResnet]) or increasing the number of channels.

As my challenge, identification of salt in images, was a segmentation problem, I followed [Unet] approach: first reduce the resolution of the image by downsampling while increasing the number of channels (encoding), then perform convolutions on reduced resolution image with large number of channels, and after that increase the resolution by upsampling while decreasing the number of channels (decoding). For examples, see Figures 2-4.

Thus, I needed upsamplings in my strict resnet model. As they were not mentioned by [StrictResnet], I had to decide how to do them.

My approach was to use strided convolutions for downsampling and strided transposed convolutions for upsampling, both without activations. As I mentioned above, this does not interfere with the non-saturation property of strict resnets.

Strided convolutions and transposed convolutions cause the checkerboard trouble, as follows.

Checkerboard

The problem

The term comes from [Checkerboard].

It refers to checkerboard artifacts that appear on images that are produced from lower resolution descriptions by upsampling using transposed convolutions.

This paper also mentions more complicated artifacts that are created by gradients in downsampling convolutions.

According to [Checkerboard], the root of the problem lies in the fact that for upsampling and downsampling we use convolutions whose kernel sizes are not divisible by their strides.

Stride (2, 2) downsampling

As I followed the Unet approach, I wanted to reduce the resolution of my images from 101×101 to 51×51, then to 26×26, then to 13×13, and after that increase it back to 101×101.

Downsampling from 26×26 to 13×13 can be done by a 2×2 convolution, and upsampling back can be done by a 2×2 transposed convolution.

However, all other downsamplings and upsamplings cannot be done by 2×2 convolutions and transposed convolutions without padding images to a larger even size.

My approach in these cases was not to pad my images but rather use 3×3 convolutions for downsampling and 3×3 transposed convolutions for upsampling, both with stride (2, 2).

For this reason, I had to deal with convolutions whose kernel sizes were not divisible by their strides.

If networks having such convolutions produce artifacts described in [Checkerboard] and cannot be trained to avoid them, this would mean that they would not be able to predict salt correctly; this would affect my training metrics negatively.

Analysis

When upsampling is done by a transposed convolution, different parts of the convolution kernel produce different pixels in the output.

For example, if the transposed convolution is 1-dimensional with kernel size = 3, kernel = (a, b, c), and stride = 2, then b is applied to the pixels that correspond to the pixels of the original image, and (a, c) are applied to produce the newly added intermediate pixels; see Figure 5.

In our case stride = 2 and the kernel is divided into two subkernels, b and (a, c). As the kernel size = 3 is not divisible by the stride = 2, these subkernels have different sizes, 1 and 2.

For a 2-dimensional 3×3 transposed convolution with stride = (2, 2), the partition is as follows: the center pixel of the kernel gets a 1-element subkernel, the pixels which are in the middle of the edges of the kernel get 2-element subkernels, and the corner pixels get a 4-element subkernel; see Figure 6. In this case, the disparity in the size of the subkernels is much more pronounced: the largest subkernel is four times larger than the smallest one.

It appears to me that the checkerboard problem is caused by the fact that the smaller subkernels underfit: they are inadequate to produce the images.

The approach of [Checkerboard] is to equalize the subkernels by special algorithms. For example, for a 1-dimensional convolution with kernel = 3 and stride = 2, they suggest an algorithm they call nearest-neighbor-resize convolution. This algorithm splits the three elements (a, b, c) of the kernel into two subkernels equally: one subkernel is (a + b, c) and the other is (a, b+ c), so that each has two elements but the 4 elements they have together, are linearly dependent.

My approach

As I see the problem in smaller subkernels underfitting, I suggest increasing the kernel size to make all subkernels large enough to fit. Such change would increase the smaller subkernels making them sufficiently expressive. In addition, it would make the disparity in the size of the subkernels less pronounced. For example, a 5×5 kernel with stride (2, 2) would have subkernels of sizes 4, 6 and 9; the largest subkernel is 2.25 times larger than the smallest one, as opposed to 4 times in the case of a 3×3 kernel.

Instead of using for upsampling a 3×3 transposed convolution with stride (2, 2), I suggest using the next larger symmetric kernel, 5×5.

Thus, I suggest a transposed 5×5 convolution with stride (2, 2).

An alternative to it is a sequence of a 3×3 transposed convolution with stride (2, 2) and then a 3×3 convolution with stride (1, 1). If this is not enough, we can apply another 3×3 convolution with stride (1, 1) to the result.

Similarly, for downsampling I suggest a sequence of 3×3 convolutions, the last of which has stride = (2, 2) and the ones before it have stride = (1, 1).

Figure 2 shows these sequences as the downsampling and the upsampling blocks.

Such design greatly simplifies the algorithms.

My tests

I have compared the effect of the additional convolutions at each upsampling and downsampling with adding a comparable number of resnet blocks: one resnet block vs. adding two convolutions at upsampling or downsampling. Most of the results showed no difference with one test showing a preference for additional convolutions inconclusively (the size of the difference was close to the range of random variations of the results, see Variance of training results below).

These results mean that the checkerboard phenomenon is present, as the effect of a resnet block which includes also activations in addition to the two convolutions, can be achieved by two convolutions without activations.

However, this effect appears to be minimal.

Conclusion

I have studied downsampling of odd-sized images to half size (101×101 to 51×51 and 51×51 to 26×26) and upsampling them back.

To be on the safe side, I recommend performing it as follows.

For downsampling, use two 3×3 convolutions followed by a 3×3 convolution with stride (2, 2).

For upsampling, use a 3×3 transposed convolution with stride (2, 2) followed by two 3×3 convolutions.

Batch normalizations

I have already mentioned above that the non-saturation property of strict resnets allows for batch normalizations on the main information path.

I have compared Unets which have one batch normalization before the final sigmoid activation, and no more batch normalizations in the main information path, with Unets that also have batch normalizations after each upsampling and downsampling.

The latter generally had better results, with one exception; it is mentioned in My experience initializing strict resnets below.

Figures 2 and 3 show the architecture of these Unets.

As I saw that adding batch normalizations improves the results, I tried to add batch normalization between all resnet blocks as shown in Figure 7. The result was unexpected: the learning started on a plateau. It did not proceed, and all my convergence metrics did not improve at all.

I did not research further the reason for this phenomenon. See Batch normalizations after each block below for my guess why this happened.

Initializers: Glorot and He

To understand this subject, we need a digression into its history.

Glorot

Assumptions

[Glorot_Initializers] studied the initialization of weights of neural networks from the points of (1) avoiding saturation and (2) avoiding vanishing and exploding gradients.

This paper assumes a straight feedforward architecture of a tower of linear fully connected layers, each followed by an activation layer.

The activation function is assumed to be either a hyperbolic tangent, or the softsign f(x) = x / (1 + |x|) , or similar; it is linear and close to the identity function for small values of x and saturates for large values of x.

This paper assumes that the weights of each layer are initialized randomly and independently using the same random distribution, and recommends to set the variance of this distribution as follows.

Avoid saturation

To keep the activations within the linear range of the activation function and avoid saturation, we need to make sure the application of each weight layer together with its activation preserves the variance of the activations.

Specifically, this paper considers a sequence of fully connected linear weight layers and activation layers, and it strives to keep the variance of the output of the activation layers constant.

As the activation layers are multidimensional and the activation function is applied to each component separately, we strive to keep the variances of the components equal for all layers.

As long as we are in the linear range of the activation function, the activation layer does not change the variances. For this reason, to keep the variances constant, we need to make sure that the weight layers do not change the variances of the components.

How to initialize the weights

This paper argues that the value of the variance of the weights of a layer that is necessary for this, is 1/n where n is the size – the number of input features – of the layer.

For this value of the variances of the weights and under our assumptions, the application of the weight layer preserves the variances of the components.

For convolution layers, this argument needs to be modified to account for the fact that the layer is not fully connected; for a 2-dimensional convolution, we should take n = kernel_height * kernel_width * number_of_input_channels where number_of_input_channels is the number of channels in the layer.

Avoid vanishing and exploding gradients

On the other hand, to avoid vanishing or exploding gradients, the same variance should be close to 1/n_next where n_next is the number of the output features of the layer, i.e., the size of the next layer; for a 2-dimensional convolution layer, we take n_next = kernel_height * kernel_width * number_of_output_channels where number_of_output_channels is the number of channels of the next layer.

Compromise variance

As a compromise between the values 1/n and 1/n_next , this paper suggests using the value 2 / (n + n_next) for the variance of the initialization weights.

The paper suggests to use the uniform distribution on an interval [-a, a] where a = sqrt(6 / (n + n_next)) ; Keras refers to this initialization as glorot_uniform .

Keras also gives another possibility which it calls glorot_normal ; it is the truncated normal distribution with the same value of variance.

Same feature space

Consider the case of a weight layer operating in the same feature space; this implies that n = n_next .

If such layer is glorot_... initialized, then the variance of the initialization weights is 2 / (n + n_next) = 1 / n .

We have seen above that a weight layer initialized this way, preserves the variances of the components.

Thus, if a glorot_... initialized weight layer does not change its feature space, then it does not change the variances of the components.

He

[He_Initializers] extended these results to Rectified Linear (relu) activation f(x) = max(0, x) .

In this case we are not concerned with growing activation values since they are not related to saturation.

As for vanishing and exploding gradients, this paper argues that the variance of the distribution of the initial values should be 2/n_next for relu activations instead of 1/n_next , to compensate for the fact that the relu activation halves the variance.

This yields initializers that Keras calls he_uniform and he_normal : he_uniform is the uniform distribution on an interval [-a, a] where a = sqrt(12) / (n + n_next)) , and he_normal is the truncated normal distribution with the variance 2/n_next .

We note that in case n = n_next the variances of the he_... initializers are twice more than those of the glorot_... ones. This implies that the application of a weight layer initialized this way, doubles the variances of the components.

Effect of batch normalization

[BatchNormalization] introduced batch normalizations which made the arguments of [Glorot_Initializers] and [He_Initializers] irrelevant for batch normalized networks.

Indeed, if we insert batch normalizations into straightforward towers of linear weight layers and activations that were the subject of [Glorot_Initializers] and [He_Initializers], this prevents growth and decay both of the activation values and the gradients.

And indeed, [BatchNormalization] reports reduced dependence of training and gradient flow on initialization.

Resnets

All the above arguments – including the independence of the initializers in the presence of batch normalizations – assume straightforward towers of linear weight layers, activations and possibly batch normalizations.

These results may be unaffected by a few skip connections. However, resnets have multiple skip connections and these arguments are not applicable to them; we cannot assume that resnets, even though they are batch normalized, are indifferent to the choice of initializers.

My experience initializing strict resnets

Generally, training with glorot_normal yields better results than with glorot_uniform , and both are better than he_normal and he_uniform .

For one test the model in Figure 3 with he_normal initializer failed as it started training on a plateau; it succeeded after I changed the initializer to glorot_uniform .

I have reported above that I found it better to keep batch normalizations at each downsampling and upsampling rather than remove all batch normalizations from the main information path. Here I noticed an exception: the failed model did have batch normalizations at each downsampling and upsampling but after I removed all batch normalizations from the main information path and replaced the he_normal initializer by he_uniform, the training succeeded.

For the models in Figures 2 and 4 training with he_normal and he_uniform initializers succeeded although its results were worse than with glorot_... initializers.

Discussion

What I do not understand

I have encountered above the following three phenomena for which I have no explanation:

1. For strict resnets, glorot_normal and glorot_uniform initializers are better than he_normal and he_uniform.
2. When I inserted batch normalization after each resnet block, the learning started on a plateau and did not advance.
3. On the other hand, inserting batch normalizations on the main information path sparingly (on each upsampling and downsampling in my tests) helps convergence in comparison with no batch normalizations on the main information path until the one before the last sigmoid.

Related to initialization

These three phenomena are related to initialization and the initial training step, as follows.

The first one involves initialization; for the second and the third ones I have a guess that explains them in the way that involves the initial training step; see below.

How initialization affects training

If the initial values are too far from good solutions, training may not arrive at these solutions. In our discussion, we shall try to analyze in what sense the initial values may be too far from good solutions.

Initial training step: comparison of different contributions

We shall discuss here how different initializations and batch normalization architectures affect the initial training step.

We shall see the difference in the way different parts of the network contribute to the prediction probabilities on the initial training step.

For some setups, some parts contribute more and for others, other parts contribute more. If such breakdown of contributions turns out to be too far from good solutions, training may not arrive at them.

We shall see how differences in network designs affect both the training results and the breakdowns of these contributions.

For lack of better explanation, I conjecture that the differences in training results are related to the differences in the breakdowns of the contributions.

My data do not allow me to make a stronger conclusion.

A geometric study of strict resnets

Summands

Recall that all resnet blocks in our networks operate on the same feature space until downsampling or upsampling.

The contribution of each resnet block is added to the result of the previous step; see Figure 8 for a picture in the feature space.

Our networks are structured as follows.

They start with the initial convolution that transforms the input into the feature space.

They apply a sequence of resnet blocks, downsamplings and upsamplings to the output.

The result is fed to the final block that includes the final convolution, the batch normalization and the sigmoid.

In other words, we start with the output of the initial convolution and apply a sequence of the following operations to it:

• Adding contribution of one resnet block.
• Transformation of the feature space: downsampling or upsampling.

The result is supplied to the final block that produces the prediction probabilities.

In other words, we sum up the output of the initial convolution and the contributions of resnet blocks until we get to a transformation of the feature space.

Whenever we transform the feature space, we apply the transformation both to the sum and to each summand accumulated already. In this way, all these summands become vectors in the new feature space, and we add the contributions of the new resnet blocks to them.

Comparing contributions

We compare the magnitudes of these summands in all feature spaces.

In particular, we compare the magnitudes of these summands in the last feature space where the sum is the input to the final convolution.

Different initializations and different arrangements of batch normalizations on the main information path in our models result in different ways this sum is broken into individual summands.

I guess that for some of the settings the initial breakdown of our sum may be so far from good solutions that the learning may not arrive at them, either starting on a plateau or getting to a worse minimum point of the loss function.

(The magnitude of the entire sum is immaterial since we batch normalize it before applying the final sigmoid to it; only the relative contributions of the summands to the sum are essential.)

Comparing variances

As each summand for the initial training step is random, we compare the variances and the standard deviations of these summands as measures of their magnitudes.

Comparing variances in different feature spaces

We assume that the weights of each convolution are initialized randomly and independently using identical random distributions in a way similar to the assumptions of [Glorot_Initializers] and [He_Initializers].

Our transformations – downsamplings and upsamplings – are also random on the initial training step. Most likely, they change the magnitudes of these summands by ratios which are not far from each other.

To be precise, the variances of all summands are changed under our transformations proportionally to the variance of the sum. Indeed, our transformations are compositions of convolutions and batch normalizations. We show our statement separately for a convolution and for a batch normalization. It is clear for a batch normalization since the latter divides each component of the sum and of each summand by a non-random constant which is the standard deviation of this component in the sum. For a convolution, our statement follows by arguments similar to those of [Glorot_Initializers] and [He_Initializers].

In this way we can compare the magnitudes and the variances of the contributions in different feature spaces.

Variances are vectors

As our summands are vectors, we consider the variances of each component of these vectors.

In other words, the variances and the standard deviations of the sum and each of the summands are vectors.

Note also that since the summands are random, the standard deviation of the sum is not equal to the sum of the standard deviations of the summands; the equality holds only if the summands are fully correlated, and this is not our case. If the summands are independent, then the variance of the sum is equal to the sum of the variances of the summands; however, this is also not our case since the output of an earlier term is the input of the next one, and hence, they are correlated. Figure 8 shows the summands but neither their standard deviations nor their variances.

The variance of the output of the initial convolution

We assume that the input to the network is normalized so that the standard deviation of each of its components is 1.

From now on, we shall not repeat the words each of its components each time and understand that variances and standard deviations are taken of each of the components of each random vector in question.

For the initial convolution we have number_of_input_channels = 3 while number_of_output_channels = 16 for the networks shown in Figures 2 and 4, and number_of_output_channels = 12 for the network shown in Figure 3.

This implies that in the case of glorot_... initialization, the standard deviation of the output is sqrt(6/19) ≈ 0.56 for the networks shown in Figures 2 and 4, and sqrt(2/5) ≈ 0.63 for the network shown in Figure 3.

Indeed, we have seen that if the variance of each of the weights of a convolution layer is 1/n, then the variance of the components of its output is equal to the variance of components of its input.
For glorot_... initialization, the variance of the weights is 2 / (n + n_next); it is different from 1/n and hence, the convolution multiplies the variances of the components by
(2 / (n + n_next)) / (1 / n) = 2 * n / (n + n_next).
As the variance of the components of the input is 1, the standard deviation of the components of the output is sqrt(2 * n / (n + n_next)).
Recall that n = kernel_height * kernel_width * number_of_input_channels, n_next = kernel_height * kernel_width * number_of_output_channels and number_of_input_channels = kernel_height = kernel_width = 3; this implies that n = 27.
For the networks shown in Figures 2 and 4, number_of_output_channels = 16; thus, n_next = 144 and the standard deviation of components of the output is
sqrt(2 * n / (n + n_next)) = sqrt(2 * 27 / (27 + 144)) = sqrt(6/19) ≈ 0.56.
For the network shown in Figure 3, number_of_output_channels = 12; thus, n_next = 108 and the standard deviation of components of the output is sqrt(2 * n/(n + n_next)) = sqrt(2 * 27 / (27 + 108)) = sqrt(2/5) ≈ 0.63.

For he_... initialization, the standard deviation of components of the output is sqrt(3/8) ≈ 0.61 for the networks shown in Figures 2 and 4, and sqrt(1/2) ≈ 0.71 for the network shown in Figure 3.

Indeed, the argument is similar to the argument in the case of glorot_... initialization.
In this case the variance of the weights is 2/n_next. It is different from 1/n and hence, the convolution multiplies the variances of the components by
(2 / n_next) / (1 / n) = 2 * n / n_next.
As the variance of the components of the input is 1, the standard deviation of the components of the output is sqrt(2 * n / n_next).
We have already seen that for the networks shown in Figures 2 and 4, n = 27 and n_next = 144; hence, the standard deviation of components of the output is
sqrt(2 * n / n_next) = sqrt(2 * 27 / 144) = sqrt(3/8) ≈ 0.61.
For the network shown in Figure 3, n = 27 and n_next = 108; hence, the standard deviation of components of the output is sqrt(2 * n/ n_next) = sqrt(2 * 27 / 108) = sqrt(1/2) ≈ 0.71.

We see that in all our cases the standard deviation of the output of the initial convolution is between 0.56 and 0.71.

The variance of the contribution of one resnet block

In analyzing it, we start with the second batch normalization of the resnet block, see Figure 1.

The variance of its output is 1.

The variance of the output of the relu that follows it, is 1/2.

The last weight block operates in the same feature space; we have seen above that this implies that it preserves the variances if its initializer is glorot_... , and doubles them if its initializer is he_... .

It follows that the variance of its output is 1/2 if its initializer is glorot_... and 1 if its initializer is he_... ; this is the variance of the contribution of this resnet block.

The standard deviation is sqrt(1/2) for glorot_... initializer and 1 for he_... initializer.

We note that this is independent of the variance of the input to this resnet block.

The variance after a batch normalization on the main information path

We may include the batch normalizations on the main information path, either at downsamplings and upsamplings, or after each resnet block.

As our convolutions are initialized randomly, the expectation of their outputs is zero. This includes the outputs of the initial convolution and each resnet block.

Thus, all vectors on the main information path are random with distributions centered at zero.

For this reason the effect of the batch normalization on the main information path is to divide each component of its input by its standard deviation.

We have already mentioned that for each transformation of feature space, we apply the transformation both to the sum and to each summand accumulated already.

In particular, the input to a batch normalization is the sum of terms accumulated earlier, and we apply it both to the sum and each of the summands.

Thus, a batch normalization divides each component of these summands by the standard deviation of the similar component of their sum.

For a picture in the feature space, see Figure 9.

The variance after transformation of feature space

We transform the feature space on downsampling and upsampling as shown in the respective blocks in Figure 2; in some of my tests, I had only two convolutions in these blocks instead of the three shown in Figure 2.

The way a downsampling or upsampling block affects the variances and standard deviations, depends on a number of details, and here is their list:

• The initializers for the convolutions. The initializers affect the standard deviations in the following way:
  • glorot_... initializers for the strided convolution/transposed convolution that performs downsampling/upsampling and changes the number of channels. In this case, this convolution doubles the number of channels for downsampling and halves it for upsampling. A calculation similar to the one we did for The variance of the output of the initial convolution shows that this convolution decreases the standard deviation for downsampling and increases it for upsampling, both by about 20%.
  • glorot_... initializers for other convolutions. In this case, these convolutions do not change the number of channels and do not change the standard deviations.
  • he_... initializers for the strided convolution/transposed convolution that performs downsampling/upsampling and changes the number of channels. In this case this convolution doubles the number of channels for downsampling and halves it for upsampling. A calculation similar to the one we did for The variance of the output of the initial convolution shows that this convolution does not change the standard deviation for downsampling and doubles it for upsampling.
  • he_... initializers for other convolutions. In this case, these convolutions do not change the number of channels and increase the standard deviations 40% each (multiply it by sqrt(2)).
• The number of convolutions besides the stride 2 convolution/transposed convolution that performs downsampling/upsampling and changes the number of channels. In my tests this number was 1 or 2. In the case of he_... initializers, each of these convolutions increases the standard deviation as above.
• Batch normalization: whether it is included in the block, and if yes, where. In my tests, if I included it, I included it either after the last convolution of the block, or for some upsampling blocks with glorot_... initializers, I inserted it after the strided transposed convolution and before the other convolutions in the block. It follows that if I included it in my tests, the standard deviation of the output of the block was 1.

To summarize, the standard deviation of the accumulated sum after downsampling and upsampling is as follows:

• If the block includes batch normalization in my test then the standard deviation of its output is 1.
• If the block does not include batch normalization and the initializers are glorot_... then the standard deviation of its output is close to the standard deviation of its input (±20%).
• If the block does not include batch normalization and the initializers are he_... then the standard deviation of its output is greater than the standard deviation of its input 1.4 to 4 times as above (1.4 to 2 times for downsampling and 2.8 to 4 times for upsampling).

Summands vs. their sum

We have seen how to find the standard deviation of the accumulated sum after downsampling and upsampling.

As we have explained above, the terms of the sum are transformed proportionally to the entire sum:
st_dev(summand_after_transform) = st_dev(summand_before_transform) * st_dev(sum_after_tranform) / st_dev(sum_before_transform) .

In case downsampling or upsampling includes a batch normalization, st_dev(sum_after_tranform) = 1 and
st_dev(summand_after_transform) = st_dev(summand_before_transform) / st_dev(sum_before_transform) .

This equality means that to find how each summand is transformed, we need to know how the standard deviations of the summands are related to the standard deviation of the sum.

The summands are partially correlated, i.e., their correlation is between 0 and 1. Indeed, we have already explained this above, as follows. They are not fully correlated (i.e., their correlation is less than 1) since they contain weights which are independent one from the other. On the other hand, they are not independent since the output of each resnet block is the input of the other.

In case we have m summands each having standard deviation 1, this implies that the standard deviation of the sum is between sqrt(m) and m .

In the general case, if the standard deviations of the summands are std1, ..., stdm and the standard deviation of the sum is std_sum then
sqrt(std12 + ... + stdm2) ≤ std_sum ≤ std1 + ... + stdm .

These inequalities show how the standard deviations of the summands are related to the standard deviation of the sum. They allow us to find how the standard deviation of each summand is transformed by a downsampling or an upsampling which includes batch normalization.

Batch normalizations after each block

Their effect on the initial training step is as follows.

For each n, we batch normalize the sum of the first n terms: the output of the initial convolution and the contributions of the first n – 1 resnet blocks.

The standard deviation of the result is one, and we add to it the contribution of the n-th resnet block; its standard deviation is ≈ 0.7 in the case of glorot_... initialization and 1 in the case of he_... initialization.

For glorot_... initialization, the standard deviation of the sum is between sqrt(12 + 0.72) ≈ 1.22 .

For he_... initialization, 1 + 0.7 = 1.7 , and in the second one it is between sqrt(12 + 12) ≈ 1.4 and 1 + 1 = 2 .

This sum is batch normalized again; this means that it is divided by its standard deviation together with all its summands.

In other words, each of the earlier summands is divided by a number which is no less than 1.22.

After n blocks, the contribution of the first one is divided by at least 1.22ⁿ.

Downsampling or upsampling transforms all the summands to a new feature space; the batch normalization that follows this transform affects all the summands as described above.

As a result, the relative contributions of the last resnet blocks are much larger than the relative contribution of the output of the initial convolution and the first resnet blocks.

The gap between the size of the contribution of last blocks, on one hand, and of the output of the initial convolution and the contributions of first blocks, on the other, is larger for deeper networks.

This is in contrast to networks that do not have batch normalization after each block but rather either do not have them at all along the main information path or have them sparingly: for such networks, the gap between the contributions of the first and the last blocks is much less.

It appears that for deep networks, the initialization we have described here, is far away from any solution; this may explain that the learning starts on a plateau.

No batch normalizations at all between blocks

In this case, the downsampling and upsampling blocks do not include batch normalizations.

Then the standard deviations of the contributions of all resnet blocks are close to each other and to the output of the initial convolution. The standard deviation of the output of the initial convolution is between 0.56 and 0.71, and the standard deviation of the contribution of one resnet block is 0.71 or 1.

Downsampling and upsampling may increase the standard deviations of earlier summands a few times. This happens only for he_... initialization.

As the result, the standard deviations of the contributions of all resnet blocks are close to each other, with later ones possibly having smaller values.

However, if we consider the effect of the weights of the earlier resnet blocks, it is much more significant since they not only affect the contributions of their blocks but also the inputs of later blocks, and the contributions of these later blocks through their inputs.

For comparison, for networks which have batch normalizations on downsampling and upsampling, these batch normalizations decrease the contributions of earlier blocks and thus mitigate the effect of their weights.

It appears that for networks without batch normalizations on the main information path, our initializations, glorot_... and he_... , are further from a good solution and for this reason learning arrives at a worse one.

Why glorot_... is better than he_...

Downsampling and upsampling include batch normalization

We first consider the case when downsampling and upsampling include batch normalization; this implies that each downsampling and upsampling decreases the standard deviations of all earlier terms so that the standard deviation of their sum is 1.

We have seen above that the standard deviation of the output of the initial convolution is between 0.56 and 0.71.

The standard deviation of the contribution of each resnet block is about 0.71 in the case of glorot_... initialization; this is more than the standard deviation of the initial convolution although the gap between the two is not significant.

In the case of he_... initialization, the standard deviation of the contribution of each resnet block is 1; this is at least 40% more than the standard deviation of the initial convolution.

When we get to downsampling or upsampling, the standard deviations of the terms accumulated this far decrease by being divided by the standard deviation of the accumulated sum. The new terms after that have equal standard deviations (0.71 for glorot_... initialization and 1 for he_... initialization) until the next downsampling or upsampling, and so on.

In the case of he_... initialization, each term after a downsampling or an upsampling has the same standard deviation as the sum of the terms accumulated before this downsampling/upsampling while in the case of glorot_... initialization, it is only 71% of the standard deviation of this sum.

For this reason, the standard deviations of the terms decrease faster with downsamplings and upsamplings in the case of he_... initialization than in the case of glorot_... initialization.

Consider the sequence s0, s1, s2,... of the standard deviations of the terms; here s0 is the standard deviation of the output of the initial convolution and sn for n > 0 is the standard deviation of the contribution of the n-th resnet block.

We have seen that in both cases of glorot_... and he_... initializations, s0 < s1 ≥ s2 ≥ ...

However, this sequence is steeper in the case of he_... initialization than in the case of glorot_... initialization: both the increase from s0 to s1 is steeper and the decrease afterward is faster.

It appears that the less steep version created by glorot_... initialization is better; it is likely to be closer to good solutions.

Downsampling and upsampling do not include batch normalization

In this case each downsampling and upsampling changes the standard deviations of the accumulated summands insignificantly (±20%) for glorot_... initialization, and increase these standard deviations a few times for he_... initialization.

In other words, for glorot_... initialization, the standard deviations of the terms after each downsampling/upsampling are close to those before it, while for he_... initialization the standard deviations of the terms after each downsampling/upsampling are a few times less than those before it.

Similarly to the previous case, the standard deviation of the output of the initial convolution is between 0.56 and 0.71 while the standard deviation of the contribution of first resnet blocks is about 0.71 (this is close to 0.56 – 0.71) for glorot_... initialization and 1 (this is at least 40% more than 0.56 – 0.71) for he_... initialization.

Consider the sequence s0, s1, s2,... of the standard deviations of the terms as in the previous case.

For glorot_... initialization, each next term in this sequence is close to the previous one.

However, for he_... initialization, we have s0 < s1 ≥ s2 ≥ ... with a sharp increase (at least 40%) from s0 to s1 and a sharp decrease (a few times) at each downsampling and upsampling.

It appears that the latter initialization is further from a good solution.

Why glorot_normal is better than glorot_uniform

If we initialize the weights using glorot_uniform then the contributions from each resnet block have thicker tails since the tail of the uniform distribution is thicker than the tail of the truncated normal distribution with the same standard deviation.

I guess that for a deep model, the contribution of some of the blocks is large in magnitude due to thicker tail, making it further from a good solution.

Conclusion

Training of deep resnet models is sensitive to weight initialization.

The current initialization patterns have been developed for other network architectures.

In some cases, they work for deep strict resnets, and in others, they do not; this is a matter of luck rather than design.

For this reason it may be worth exploring other ways of initializing the weights for deep strict resnets, possibly individually for each resnet block.

It may be that the loss function I used, exacerbated the training difficulties I reported; even if this is the case and better-behaved loss functions present fewer difficulties, it is worth paying attention to the phenomena listed above, in case they still affect training results.

Here is the report on my loss function.

My loss function may have strengthened all these phenomena

The evaluation criteria of the competition was a variation of Intersection over Union (IoU) of the ground truth and prediction, averaged over all samples.

The ground truth is the pixel matrix with value 1 for each pixel indicating salt, and 0 otherwise. Prediction is the pixel matrix of predicted probabilities of salt.

I followed [RahmanWangIoU] which suggested defining IoU for ground truth and prediction probabilities as Intersection/Union where
Intersection = sum(GroundTruth * PredictionProbabilities) ,
Union = sum(GroundTruth + PredictionProbabilities - GroundTruth * PredictionProbabilities) ,
and the operations * and + are understood pixelwise.

The loss function – it is a function of the ground truth and the predicted probabilities – is defined as 1 - IoU averaged over all samples.

The loss function defined this way, is discontinuous at the point where GroundTruth = PredictionProbabilities = 0 .

At this point, the ground truth contains all zeroes (no salt), and all the prediction probabilities are zero exactly. Thus, at this point IoU = 0/0; this indeterminacy is resolved as 1 since all the predictions are correct.

However, when the ground truth is zero but the prediction probabilities are only close to 0 then there is no indeterminacy, Intersection = 0 , Union = sum(PredictionProbabilities) > 0 and IoU = 0.

Thus, the loss function is discontinuous at this point.

To avoid this discontinuity, I modified this definition by adding a smoothing ε term: IoU = (Intersection + ε) / (Union + ε) where I took ε = 0.62 to minimize the maximal difference between the smoothened IoU and the true IoU for all values of the ground truth and the predicted probabilities.

However, the loss function defined this way, did not work well: the training always started successfully but at some point it took a wrong step from which it could never recover.

I tried to increase the value of ε to 200 (with the hope that it would further smoothen the loss function) and increase the momentum of the gradient descent optimizer from 0.9 to 0.99 (with the hope that this would reduce the size of the wrong step) but neither helped.

Eventually, I modified my loss function by taking IoU not over each image but rather over all pixels in a batch of 32 images. Such modified IoU loss trained well. However, I suspect that some of the difficulties in training that are listed above, may be more pronounced for this loss function; maybe an alternative, [Lovasz] loss is less affected by these difficulties; I did not test this possibility.

Nevertheless, it seems to me that my experience is a valuable lesson to take into account; even if for another loss function the training would not fail as it did for me, it may still affect it negatively in some way.

Deep against wide

The conventional wisdom of machine learning says that for the same computational resources, better going deep that going wide.

Here are the results of my attempts to compare deep with wide.

Speed per epoch

[TimeComplexity] shows that the time to train a convolutional layer for one epoch is proportional to the product of the number of input channels (the number of channels in the layer) and the number of output channels (the number of the channels in the next layer). As in our case the number of the channels is the same if we are in the same resnet block, the time to train for one epoch is proportional to the square of the number of channels.

They also argue that for deeper networks, the training time is proportional to the number of the layers – the depth of the network.

However, their argument does not take into account that the backpropagation for deeper networks takes more time per layer since we need to find the gradients of the output of each layer with respect to the weights of all prior layers, and there are more prior layers in a deeper network.

For this reason, I expected that a deeper network would take more time to train than the estimates of [TimeComplexity] predict.

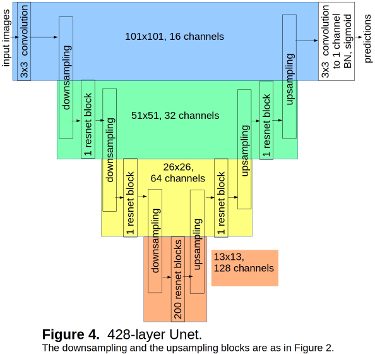
I have compared the models shown in Figure 2 (272 layers network) and Figure 3 (412 layers network); their numbers of channels in the respective layers are related 4:3 and the estimates of [TimeComplexity] suggest using the relation of 9:16 for the depths.

The model which is shown in Figure 2 had 18 resnet blocks for each Unet level, and 9:16 relation for the depths would have meant 32 resnet blocks for the equivalent deeper model.

Instead, I designed the model shown in Figure 3 with 28 resnet blocks rather than 32; nevertheless, it still trains longer: about 12.5 minutes per epoch while the model shown in Figure 2 trains about 10.5 minutes per epoch.

Number of epochs to train

One would expect that deeper and more complicated models would require more epochs to get to a solution.

I have noticed such difference but my statistics are insufficient to make any definite statement.

Variance of the training results

I observed that the training results change from one run to the other; they are random.

One would expect that the variance of the training results would be larger for a more complicated model.

My experience indicates that this is the case but my statistics are insufficient to make any definite statement.

Results

The best results achieved by the two architectures, Figure 2 and Figure 3, are close.

(The architecture in Figure 4 achieved similar results with training time similar to the architecture shown in Figure 2.)

Summary

It appears that there is little advantage of the architecture of the deeper Figure 3 over the architecture of Figure 2.

Comparing different depths

To make this comparison complete, one would want to see how the training results for the models shown in Figure 2 and Figure 3, compare with the training results for similar models of different depths with the same numbers of channels.

It could be that the training results for each architecture increase with the depth up to a certain limit, and both Figure 2 and Figure 3 are beyond these limit points.

In such case, the real comparison should be between the models at these limit points. In other words, we would need to compare the models of minimal depth that achieve the best results for each of the architectures.

I have not done such comparison.

The only similar comparison I have done is for the model in Figure 4: I have compared its performance with 100, 200 and 300 resnet blocks at the 13×13 level. There was an improvement from 100 blocks to 200 but no improvement from 200 to 300 blocks.

References

[BatchNormalization] S. Ioffe and C. Szegedy. Batch normalization: accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), 2015. [PDF] [back to Initializers: Batch normalization]

[Checkerboard] A. Odena, V. Dumoulin and C. Olah. Deconvolution and Checkerboard Artifacts, Distill, 2016. [html] [back to Checkerboard]

[Glorot_Initializers] X. Glorot and Y. Bengio, Understanding the difficulty of training deep feedforward neural networks, Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, PMLR 9:249-256, 2010. [link] [back to Initializers: Glorot] [back to Initializers: Batch normalization] [back to Discussion: A geometric study of strict resnets: Comparing variances in different feature spaces]

[He_Initializers] K. He, X. Zhang, S. Ren and J. Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV) p.1026-1034 2015. [PDF] [back to Initializers: He] [back to Initializers: Batch normalization] [back to Discussion: A geometric study of strict resnets: Comparing variances in different feature spaces]

[Lovasz] M. Berman, A. Rannen Triki, M. B. Blaschko. The Lovász-Softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. p.4413–4421 (2018) [PDF] [back to My loss function…]

[RahmanWangIoU] M. A. Rahman and Y. Wang. Optimizing Intersection-Over-Union in Deep Neural Networks for Image Segmentation. International Symposium on Visual Computing, Springer, 2016, p.234–244. [PDF] [back to My loss function…]

[Resnet] K. He, X. Zhang, S. Ren and J. Sun. Deep Residual Learning for Image Recognition, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, p.770-778. [PDF] [back to Resnet going deep] [back to Strict resnets: Changes in feature space]

[StrictResnet] K. He, X. Zhang, S. Ren, and J. Sun. Identity Mappings in Deep Residual Networks. arXiv preprint arXiv:1603.05027v3,2016. [PDF] [back to Resnet going deep] [back to Strict resnets: They never saturate] [back to Strict resnets: Changes in feature space]

[TimeComplexity] K. He and J. Sun. Convolutional neural networks at constrained time cost. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, p.5353-5360. [PDF] [back to Deep against wide: Speed per epoch]

[VGG] K. Simonyan and A. Zisserman, Very deep convolutional networks for large scale image recognition, Proceedings of ICLR 2015, p.1-14. [PDF] [back to Resnet going deep]

[Unet] O. Ronneberger, P. Fischer, T. Brox. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Lecture Notes in Computer Science, vol 9351. Springer, Cham, 2015. link [back to Strict resnets: Changes in feature space] [back to Checkerboard]

If you like this post

Please consider nominating it for The Distill Prize for Clarity in Machine Learning.